Groups
Use the Group class to treat a collection of Nodes and Links as if they were a single Node. Those nodes and links are members of the group; together they constitute a subgraph.
A subgraph is not another Diagram, so there is no separate canvas for the subgraph of a group. All of the Parts that are members of a Group belong to the same Diagram as the Group. There can be links between member nodes and nodes outside of the group as well as links between the group itself and other nodes. There can even be links between member nodes and the containing group itself.
Groups can also be collapsed and expanded, to hide or show the member parts.
The member parts of a group are available via the Group.MemberParts property. Conversely, the Part.ContainingGroup property refers to the group, if the part belongs to one. A part can be member of at most one group at a time. You can set that property in order to add that part to a group. However you must make sure that no group contains itself, either directly or indirectly through other groups.
Because every Group is a Node, you can have nested groups. Although member Nodes and Links belong to the Group that contains them, they are not in the visual tree of the group -- their GraphObject.Panel is null and no member part is in the group's Panel.Elements collection. No Part can be in the visual tree of another Part. Parts normally do belong directly to one Layer.
See samples that make use of Groups in the samples index.
Simple Groups
In a GraphLinksModel the Model.NodeDataSource holds node data, each of which might be represented by a Group rather than by a regular Node. You can declare that it should be a group by setting the IsGroup data property to true. You can declare that a node data be a member of a group by referring to the group's key as the group data property value.
Here is a group containing two nested groups as well as two regular nodes. If you move a group, its member parts move along. If you copy a group, its member parts are copied too. If you delete a group, its member parts are deleted too. If you move a member node, its containing group inflates or shrinks to cover the area occupied by all of the members.
diagram.Model =
new MyModel {
NodeDataSource = new List<NodeData> {
new NodeData { Key = "Alpha", IsGroup = true },
new NodeData { Key = "Beta", Group = "Alpha" },
new NodeData { Key = "Gamma", Group = "Alpha", IsGroup = true },
new NodeData { Key = "Delta", Group = "Gamma" },
new NodeData { Key = "Epsilon", Group = "Gamma" },
new NodeData { Key = "Zeta", Group = "Alpha" },
new NodeData { Key = "Eta", Group = "Alpha", IsGroup = true },
new NodeData { Key = "Theta", Group = "Eta" }
}
};

Groups and Links
Because Groups are Nodes, a Link may connect with a group as well as with a plain node.
Here is a simple example of four regular nodes and one group node. In this example the link from "Alpha" goes directly to the "Beta" node, but the link to "Delta" actually comes from the "Omega" group rather than from any particular member of the group.
diagram.Model =
new MyModel {
NodeDataSource = new List<NodeData> {
new NodeData { Key = "Alpha" },
new NodeData { Key = "Beta", Group = "Omega" },
new NodeData { Key = "Gamma", Group = "Omega" },
new NodeData { Key = "Omega", IsGroup = true },
new NodeData { Key = "Delta" }
},
LinkDataSource = new List<LinkData> {
new LinkData { From = "Alpha", To = "Beta" }, // from outside the Group to inside it
new LinkData { From = "Beta", To = "Gamma" }, // this link is a member of the Group
new LinkData { From = "Omega", To = "Delta" } // from the Group to a Node
}
};
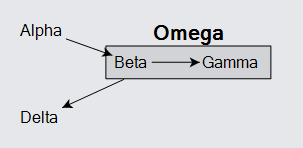
If you were to drag the "Delta" node around you would see how the link from the "Omega" group appears to come from the center of the group and starts at the group's edge rather than at any member node. This is different from the link from "Alpha" to "Beta".
Note also how the link from "Beta" to "Gamma" is effectively owned by the "Omega" group because both of the nodes are owned by that group. Copying the group automatically copies the link too.
This example did not set any of the following properties: Diagram.NodeTemplate, Diagram.GroupTemplate, and Diagram.LinkTemplate, in order to demonstrate the default templates for all kinds of node data and link data.
Group Templates
Here is an example of how one might define templates for nodes and for groups. The node template is very simple: some text inside an ellipse. The group template is different from a node template in several aspects.
First, the group template builds a Group, not a Node or Part. The group can use a number of the panel types, just as a node may use various panel types.
Second, the group template includes a Placeholder object. This object, of which you may have at most one within the visual tree of a group, gets the size and position of the union of the bounds of the member parts, plus some padding. The use of a Placeholder results in the Group surrounding the collection of group members, no matter where the member nodes are placed.
diagram.NodeTemplate =
new Node("Auto")
.Add(
new Shape("Ellipse") { Fill = "white" },
new TextBlock().Bind("Text", "Key")
);
diagram.GroupTemplate =
new Group("Vertical")
.Add(
new Panel("Auto")
.Add(
new Shape("RoundedRectangle") { // surrounds the Placeholder
Parameter1 = 14,
Fill = "rgba(128,128,128,0.33)"
},
new Placeholder { // represents the area of all member parts,
Padding = 5 // with some extra padding around them
}
),
new TextBlock { // group title
Alignment = Spot.Right, Font = new Font("Segoe UI", 15, FontWeight.Bold)
}
.Bind("Text", "Key")
);
diagram.Model =
new MyModel {
NodeDataSource = new List<NodeData> {
new NodeData { Key = "Alpha" },
new NodeData { Key = "Beta", Group = "Omega" },
new NodeData { Key = "Gamma", Group = "Omega" },
new NodeData { Key = "Omega", IsGroup = true },
new NodeData { Key = "Delta" }
},
LinkDataSource = new List<LinkData> {
new LinkData { From = "Alpha", To = "Beta" }, // from outside the Group to inside it
new LinkData { From = "Beta", To = "Gamma" }, // this link is a member of the Group
new LinkData { From = "Omega", To = "Delta" } // from the Group to a Node
}
};
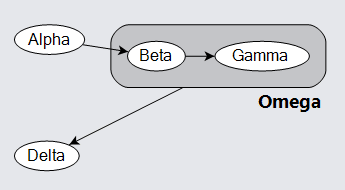
When you move the "Beta" or "Gamma" nodes, the "Omega" group automatically resizes so that the TextBlock on the group stays below and on the right side of the "RoundedRectangle" shape.
Just as a Diagram can have its own Layout, a Group can have its own Group.Layout. This is discussed in the page about SubGraphs.